Wenn jemand Bitcoins empfangen oder versenden will braucht er dafür eine Adresse. Doch woher kommt diese Adresse? Wie entsteht eine Bitcoin Adresse? Dem gehen wir in diesem Artikel auf den Grund und schauen Bitcoin mal etwas genauer unter die Haube.
Hier sieht man die, vereinfacht dargestellte, Transaktion e9a66845e05d5abc0ad04ec80f774a7e585c6e8db975962d069a522137b80c1d aus dem Block 100.000 (wer will kann sich das ganze gerne in der Bitcoin Blockchain ansehen z.B. online mit einem Blockexplorer):
from: 1JxDJCyWNakZ5kECKdCU9Zka6mh34mZ7B2 value 0,01 BTC to: 16FuTPaeRSPVxxCnwQmdyx2PQWxX6HWzhQ
Von der Adresse 1JdxD… gehen 0,01 Bitcoin an die Adresse 16Fu…
Die Schreibweise der Adresse ist jene, die man als Endbenutzer kennt. Und ist nichts anderes als die Base 58 Codierung des zweifachen Hashes des öffentlichen Schlüssels, der wiederum aus dem – geheimen – privaten Schlüssel berechnet wird. Alles klar?
Aber der Reihe nach. Am Beginn erstellt man einen privaten Schlüssel, der, wie der Name schon sagt, auf alle Fälle geheim bleiben sollte. Bitcoin benutzt für die asynchrone Verschlüsselung elliptische Kurven (Eliptic Curve Diffie Hellman – ECDHE). Man hat sich hier auf die Kurve mit dem klingenden Namen secp256k geeignet. Zur Generierung des privaten Schlüssels wird eine zufällige Zahl (P) mit einem Punkt (Q) auf der Kurve multipliziert. Der dadurch erhaltene Punkt (R) ist wiederum ein Punkt auf der Kurve und dient als öffentlicher Schlüssel.
Um das Ganze leichter zu verstehen gehen wir das mal bildlich Schritt für Schritt durch. Wir werden dabei nur oberflächlich an der dahinterliegenden Mathematik kratzen, es bleibt also noch leserlich – versprochen.
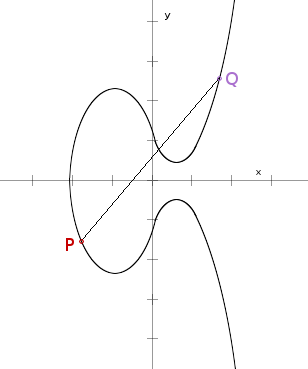
Zuerst brauchen wir den Graph dieser elliptischen Kurve, der in etwa* so aussieht:

Nun wählt man einen Punkt P der auf der Kurve liegt. Die Auswahl erfolgt zufällig, damit niemand mittels einer Regel nachvollziehen kann wo der Punkt liegt. P hat einen Zahlenwert und entspricht damit dem geheimen Schlüssel.
Ein Beispiel für einen privaten Schlüssel ist:
D9 87 3D 80 C2 D3 7D C0 FB 6A 57 78 63 33 89 F4 45 32 13 30 3D A6 1F 20 FD 67 AA 23 3F AC3 32 62

Nun wählt man noch einen Punkt Q auf der Kurve.

Mathematisch kann man nun Punkt P und Q addieren und erhält dadurch den Punkt R. Diese Funktion ist praktischerweise nicht umkehrbar (zumindest ist die Umkehrung nicht in absehbarer Zeit schaffbar, vgl. Umkehrung von Hash) und für Nichtmathematiker eventuell schon ziemlich schwer zu verstehen. Allerdings kann man diese Funktion auch graphisch als Gerade zwischen den beiden Punkten P und Q darstellen. Und schon kann man sich das Ganze auch ohne besondere mathematische Begabung vorstellen. Am Schnittpunkt der Geraden zwischen P und Q mit der Kurve erhält man den Punkt R.

Der Punkt R hat auch wieder einen Zahlenwert und entspricht nun dem öffentlichen Schlüssel, den man jedem weitergeben kann.
Durch eine geänderte Auswahl von Q, bei stets gleichem P, erhält man jedesmal einen anderen Punkt R. Damit kann man aus einem privaten Schlüssel (P) viele öffentliche Schlüssel (R) generieren. Genau das machen moderne Wallets bei jeder Transaktion – sie wechseln Q und in Verbindung mit dem privaten und gleichbleibenden P wird ein neuer Punkt R generiert. Das beständige Wechseln des öffentlichen Schlüssels dient der Steigerung der Privatsphäre.
Der öffentliche Schlüssel, der von R repräsentiert wird, ist für Menschen eine relativ lange Zahl, wie zum Beispiel dieser public key:
02 a1 63 3c af cc 01 eb fb 6d 78 e3 9f 68 7a 1f 09 95 c6 2f c9 5f 51 ea d1 0a 02 ee 0b e5 51 b5 dc
Auf den public key wird nun SHA256 und RIPEMD-160 in Serie angwandt (also zweimal ein Hash gebildet) und man erhält dann eine Bitcoinadresse im Base 58 Format:
5Kb6hWXMss8QgidDA76NzPL6TsZZY3SzNydYXYB9KFkf9zgVPno
Bitcoinadressen sind case sensitve (es wird zwischen Groß- und Kleinschreibung unterschieden) und enthalten weder ein großes O oder I ein kleines L oder die Ziffer 0. So sind sie für Menschen relativ leicht zu lesen.
Die Bitcoinadresse ist nicht besonders viel kürzer als der ursprüngliche öffentliche Schlüssel. Warum sollte man also den Schlüssel nun noch zusätzlich zweimal hashen, wo ist der Vorteil?
Dies dient der Sicherheit. Vom öffentlichen Schlüssel könnte man mit ausreichend Rechenpower den privaten Schlüssel errechnen. So viel Rechenkraft würden aber, aus heutige Sicht, lediglich Quantencomputer (die es erst einmal geben muss) bieten. Durch den doppelten Hash wird es aber auch für Quantencomputer schwer den privaten Schlüssel zu errechnen. Man müsste ja erst zweimal den Hash retour rechnen, bevor man sich an den privaten Schlüssel machen kann. Um Bitcoin gegen Angriffe von Quantencomputern sicher zu machen bedarf es allerdings noch mehr. Dafür gibt es bereits Ideen, die ich hier aber nicht näher ausführen werde. Wichtig an dieser Stelle ist, dass man als Nutzer keine Angst haben muss, wenn eines Tages – überraschend – Quantencomputer die Arena betreten. Bitcoins haben durch den doppelten Hash der Adressen einen Schutz eingebaut, der einen Vorsprung bietet, um in dieser Zeit Bitcoin weiter gegen einen solchen Angriff abzusichern.
*den Graph der Kurve habe ich sinnbildlich mit Gimp erstellt – er ist also nicht maßstäblich.